积分型ADC——原理，试制和改进

由于积分ADC及其改进型在过去的五十年中是数字万用表和电压表中最主要应用的ADC类型，所以写这篇文章来记录设计积分ADC的过程。

背景

原理

为了将电压转换为时间，我们需要构造一个有关时间的电压函数，在基本的几个电路中，显然四则运算器的响应不包含时间，而滤波器的直流响应是非线性的，只剩下微分器和积分器可选。由于我们实际上只关注直流信号，这里选用了电容积分器来构建ADC的V/T转换核心，其中选用电容而非电感是因为电感值不易控制。

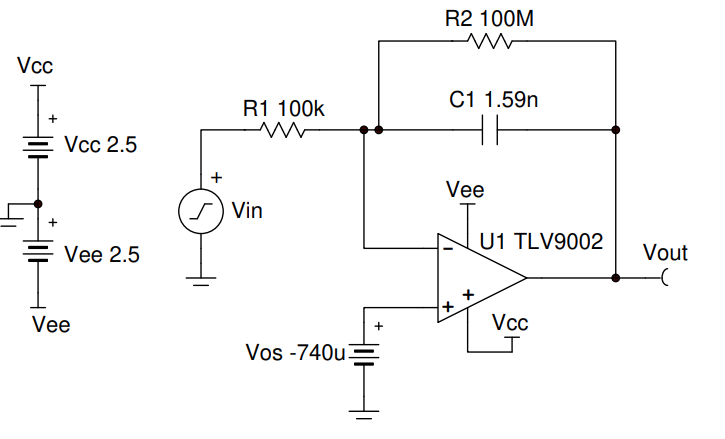
理想积分器的传递函数是：$$V_{out} = -\frac{1}{R_1C_1}\int^{T_1}_{T_0}{V_{in}(t)}dt$$ 对于直流激励则有： $$V_{out} = -\frac{V_{in}}{R_1C_1}(T_1-T_0)$$

如果我们设一个电压 $V_{th}$，当 $V_{th}=V_{out}$时，有：$$V_{in}=-V_{th}\frac{R_1C_1}{T_1-T_0}$$ 且我们知道式子右边的所有参数，则可以求解出$V_{in}$的值，这便是单斜坡积分ADC。单斜坡积分ADC使用一个比较器在 $V_{th}=V_{out}$ 时输出阶跃信号并停止计数器，以据此计算出输入的值。（可能需要另一个过零比较器以启动计数器，这里简化为了零状态启动）

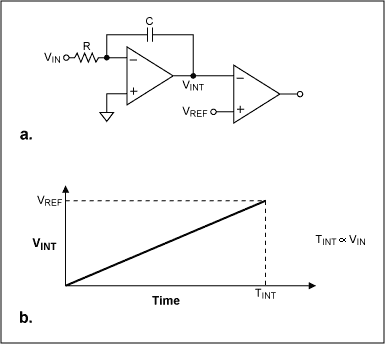
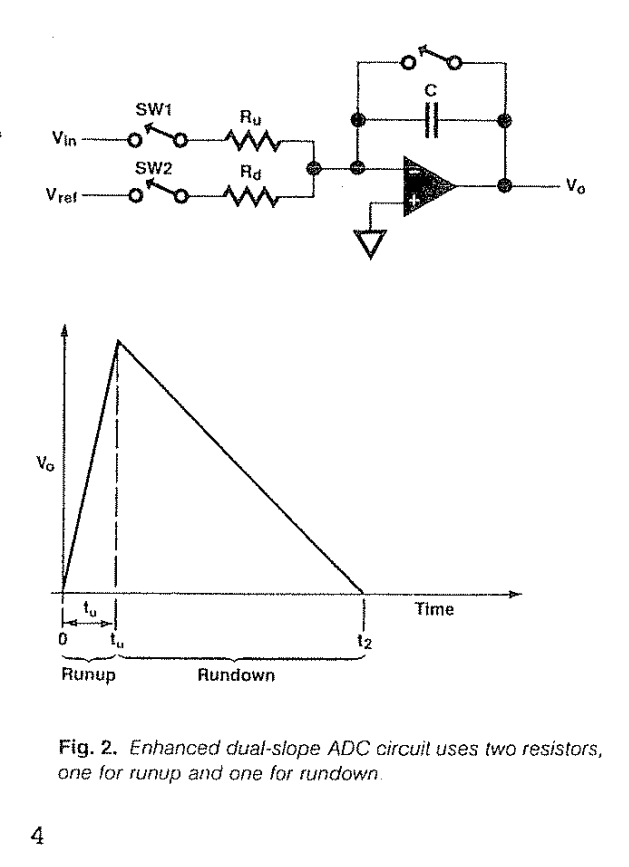
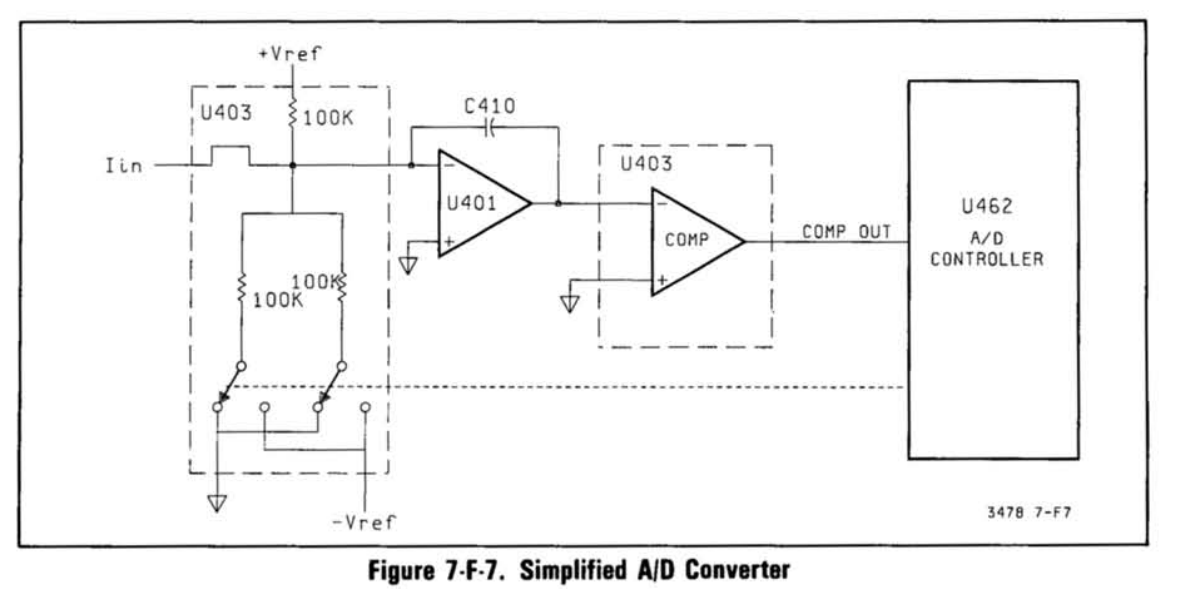
可是，这种架构十分依赖于两个被动器件 $R_1$ 与 $C_1 $的绝对值，而制造超高稳定性的电容电阻成本十分高昂，这使得这种架构精度普遍较低，因此很快衍生出了改进型：双斜坡积分ADC。在原有电路基础上添加一组开关让输入在相反极性的 $V_{in}$ 和 $V_{ref}$ 之间切换，并在 $V_{ref}$ 接通时间让电压积分归零。我们将前半接入 $V_{in}$ 的部分称为RunUp，后半部分断开 $V_{in}$ 的称为RunDown。

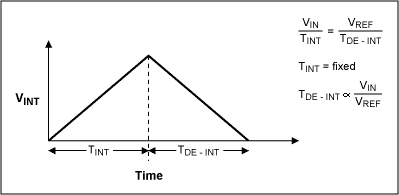
因而 $$\frac{V_{in}}{R_1C_1}(T_1-T_0)=V_{peak}=-\frac{V_{ref}}{R_1C_1}(T_2-T_1)$$ 消去$R_1$ 与 $C_1 $ $$V_{in}(T_1-T_0)=V_{peak}=-V_{ref}(T_2-T_1)$$ 整理得 $$V_{in}=-V_{ref}\frac{T_2-T_1}{T_1-T_0}$$

若$V_{ref}$是准确的且整个模拟部分系统又是理想的，该ADC的输出分辨率就是$\frac{T_2-T_1}{T_1-T_0}$即$T_1-T_0$的分辨率，而频率的精度对比电压的精度高几个数量级，据此我们只需要增加数字计数器的频率就可以显著提升分辨率，因而该种ADC在各种简单的直流电测仪器中广泛使用。稍加改进，让$V_{ref}$和$V_{in}$使用不同的斜率执行两个斜坡，最终公式为$$V_{in}=-V_{ref}\frac{T_2-T_1}{T_1-T_0}\frac{R_{vref}}{R_{vin}}$$

这将对$T_1-T_0$缩放一个$\frac{R_{vref}}{R_{vin}}$的系数并以此提升分辨率。随着膜电阻的技术发展，多个电阻可以被制作到同一个基板上，由于高度统一的制作工艺和过程，这数个电阻的漂移将高度一致。因此，这种改进方法是切实可行的。

但，双斜坡积分具有显著的缺点：

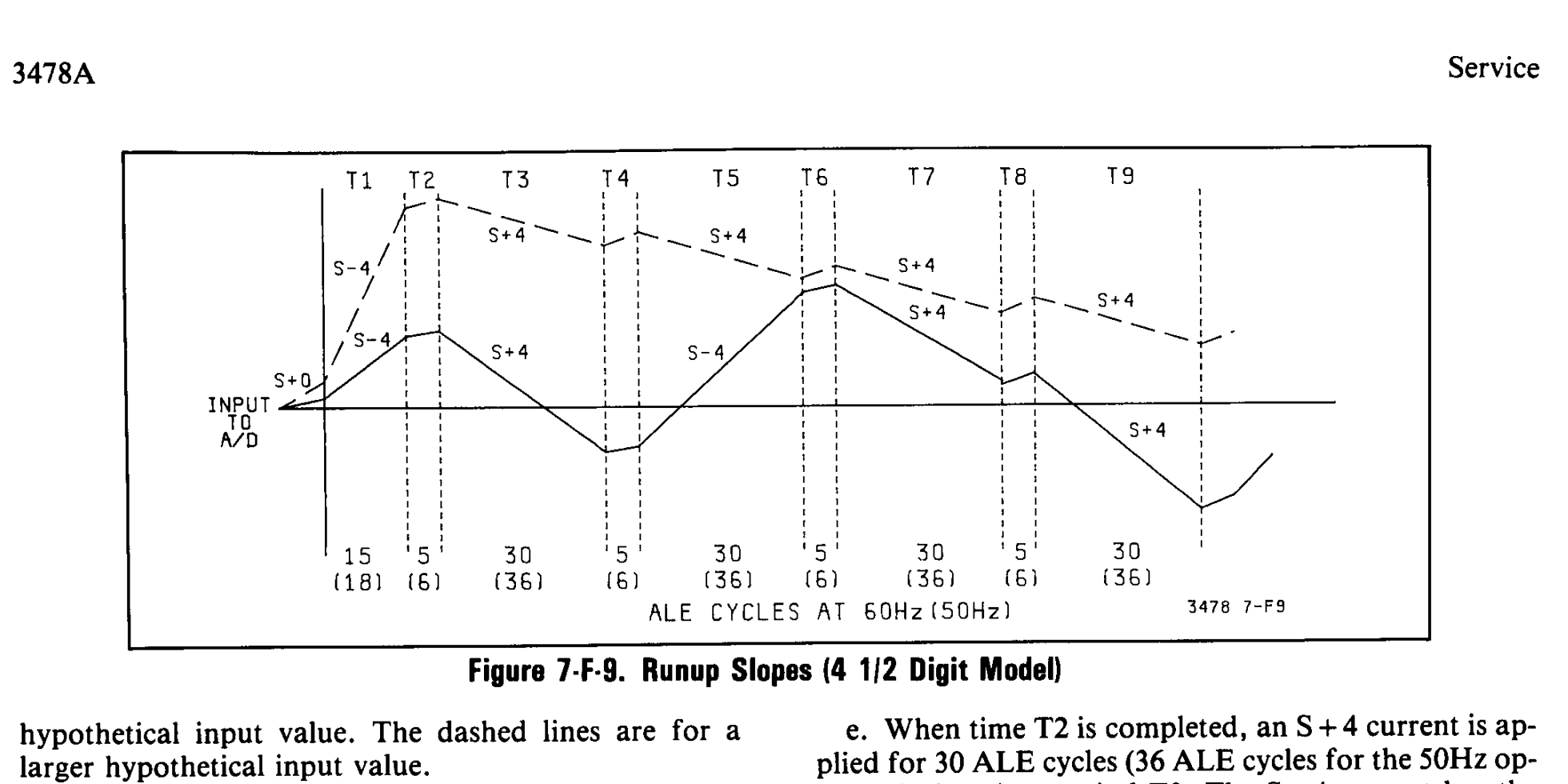
• 现实积分器受到电源轨道限制不能无限制的积分到正负无穷，且比较器的失调要求我们尽可能地使用全部的积分器动态范围（显然失调引起的误差是积分器满摆幅电压和失调电压的比），所以这种ADC的积分时长非常固定不灵活。譬如，实验室的交流电网往往会造成严重工频干扰，而全球电网的频率又不尽相同——这要求我们的输入积分时长必须是整数倍的电网周期（简写为[N]PLC，[Number of]Power Line Cycle）对于60Hz电网这是16.67ms，而对于50Hz电网这是20ms。为了不让积分器饱和，我们必须按50Hz设计积分器的时间常数，由于不能完全利用积分器的动态范围，这将导致仪器在60Hz电网下的精度折损！并且，台式万用表在实验室中往往要面对多种工况，我们不能总要求仪器以最大分辨率——往往是10NPLC或更高工作，尤其是超高精度测量在实验室中并不常见。
• 较大的阻值和电容值难以制造，并且电特性比较小的型号更差。若要达到20ms的积分时间， $R_1C_1 $ 将为 0.02，这个值听起来并不大，但考虑到1206尺寸下的C0G电容较常见的最大可选型号为100nF，这将需要200k的输入电阻。一方面，仪器内部的高阻抗源并不好，这将让仪器过度拾取环境中的噪声并严重降低指标，另一方面，若降低电阻并提高电容量，为了达到优异的电特性（甚至会达不到），这个电容将变得十分巨大，同时将有更高的漏电。

纵然我们可以制造多组成比例的电阻并以不同的斜率执行这两个斜坡以组成多斜率双斜坡积分ADC，但设计高动态范围积分器同上文所述仍是十分具有挑战的（事实上过大和过小的斜率将严重影响积分器输出级线性度，并在电阻阵列中产生不均匀的加热），将相差多个数量级的电阻集成到一起并确保互不干扰同样成本高昂。

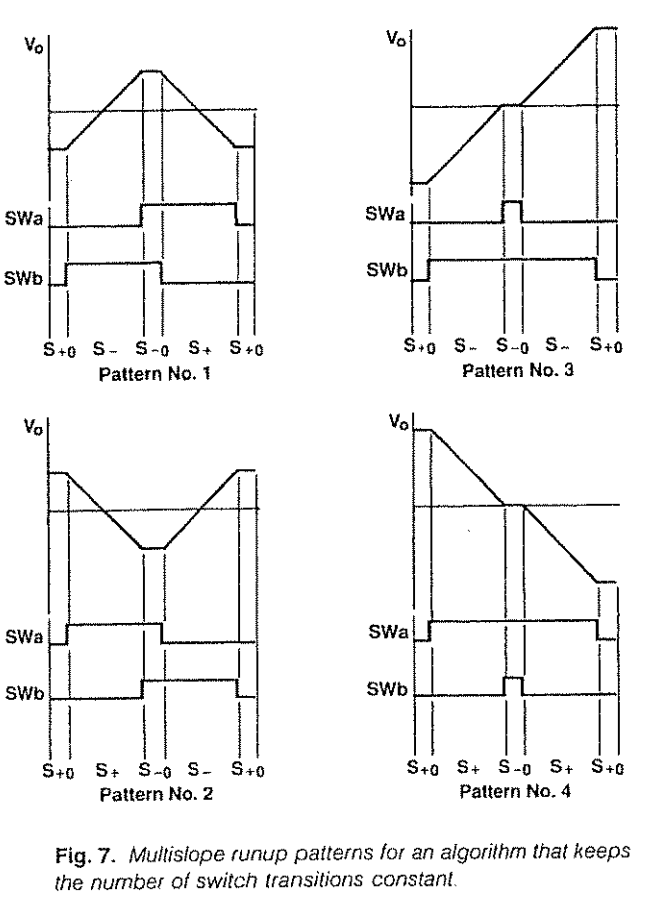
因此，一方面为了解决制造性问题，另一方面实现较为灵活的工作范围，我们采取了较小的积分器时间常数以获得小型的被动元件尺寸，并在RunUp时使用开关在$+V_{ref}$ 和 $-V_{ref}$之间切换，以控制积分电压不饱和，也就是 （注意式子右侧的残差电压）：$$\frac{V_{in}t_{in}}{t_{total}}+\frac{+V_{ref}t_{posref}}{t_{total}}+\frac{-V_{ref}t_{negref}}{t_{total}}=V_{residual}$$ 在这一阶段通常最大可使仪器获得约一半的分辨率。

由于MOSFET的电荷注入效应和开关非线性，我们在开关期间必须使用设计好的切换序列以保证MOSFET开关次数恒定且对称，一个开关模式内对称的开关方式有助于消除电荷注入减轻偏移，而一个开关模式内固定的开关次数将生成固定的非线性偏移量，该偏移量在稍后可以被校准掉。这将生成一种近似于PWM的波形，示意如下：

等待占绝大部分时间的RunUp结束后便可以在RunDown期间测量$V_{residual}$以获得剩余的一半分辨率。$V_{residual}$在模拟部分理想的情况下仅取决于量化误差、比较器延迟误差和开关延迟误差，且后两者占主要，而又因为这些误差的时间是相对固定的，我们只需要在来回过零中降低RunDown的斜率，即可降低上述误差注入的$V_{residual}$。同理，RunDown过程无法通过延长积分时间来增加分辨率，因为上述误差在斜率一定的情况下造成的$V_{residual}$是固定的。无论如何，RunDown期间将始终产生固定的分辨率，不同分辨率和积分时间的调节是RunUp提供的。

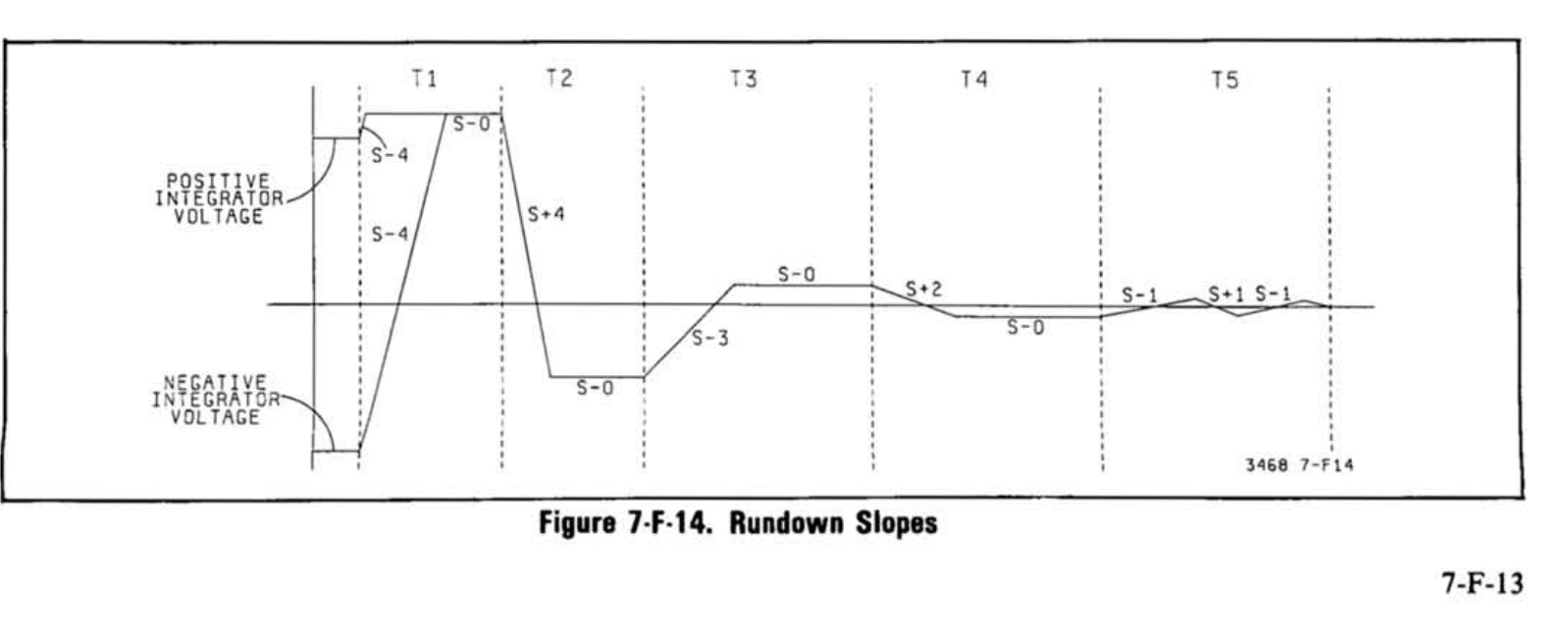
并且，由于此时$V_{in}$已经断开，我们可以使用较少的电阻并使用叠加定理创造出较多的斜率。HP3478A使用三个电阻生成了九个斜率。

据此，HP 积分ADC II的雏形已经完成，3456A、3457A、3458A、3468A、3478A均使用第二代HP积分ADC的不同变种，其中每款的具体实现细节我们将不再赘述。随着后续半导体技术的发展，34401A使用ADC取代了RunDown阶段，并持续执行RunUp并测量周期前后的积分器电压，实现了更高速的，几乎无停顿的采样。34410A更是使用ADC直接取代了比较器并使用更新的MOSFET开关以大幅提升RunUp分辨率，更新的ADC同样提升了RunDown精度，籍以实现比34401A高一个数量级的采样速度。至于更新的3446x系列，作者暂时没摸到真机，故不做讨论。

试制

Alan多斜坡ADCv1

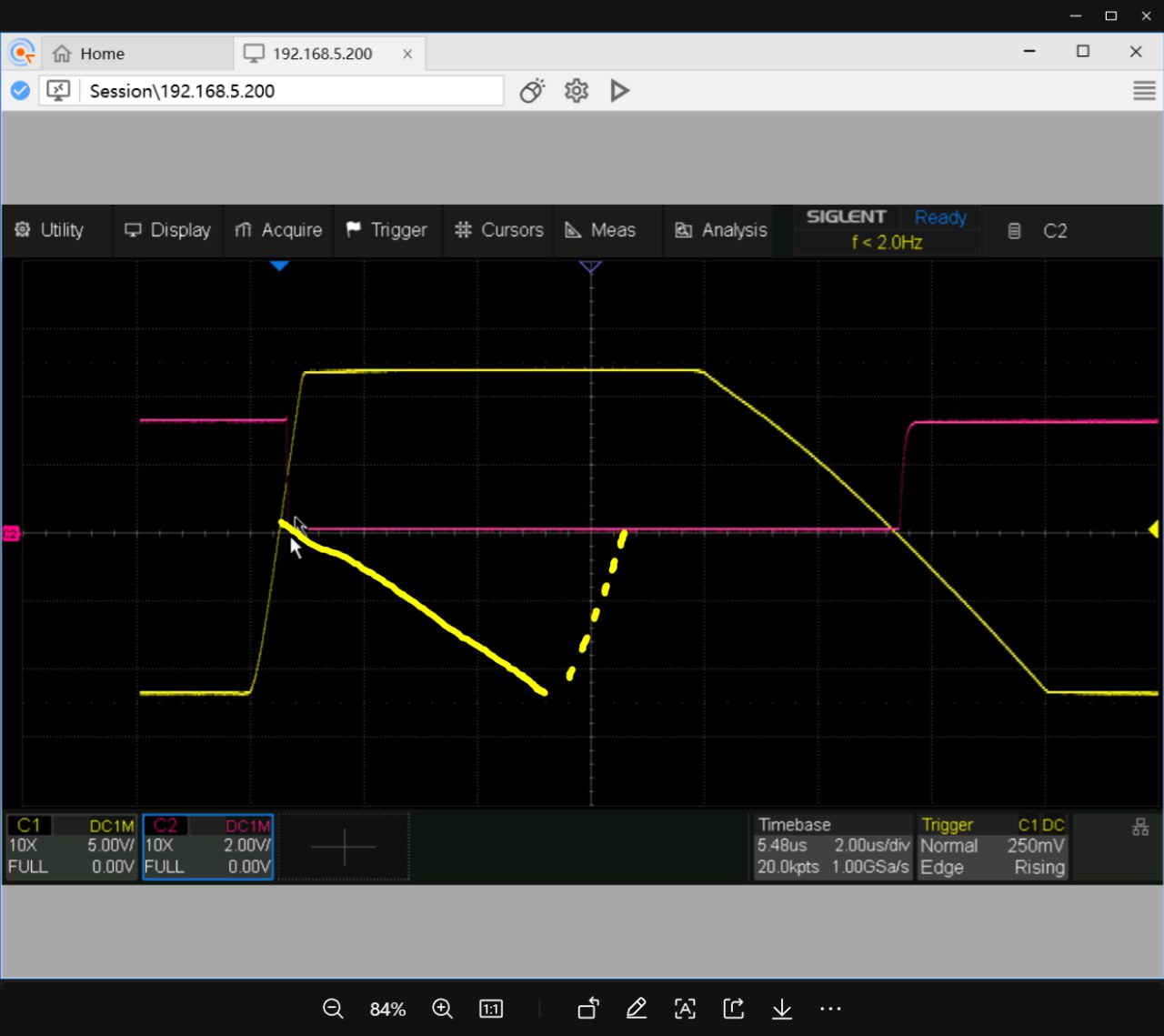
Alan多斜坡ADCv1整体模仿HP34401A，STM32硬件定时器控制，使用ADR4550与LT5400电阻网络生成+-10V基准。积分器使用LT5400电阻网络做输入74HC4053做开关，其中4053开关在不接入时将电流导入GND以避免开关上电压超过耐压，而接入时由于运放闭环，反相输入端同样为GND。电源部分使用了金升阳正负隔离模组、多重滤波和TPS7A39的组合。

该版原理图有诸多问题，譬如：LM311的输入级压摆率不高，这将产生极大的延迟，因此需要用电阻分压将输入级电压限制到较低的摆率，详见TI E2E。其次，1nF+1k的RC组合太小了，STM32中断到GPIO所需时长太长，以至于积分器直接饱和（见上图），完全无法工作。另外，输出FLASH ADC搬移电路太过复杂。

Alan多斜坡ADCv2 —— 胎死腹中

Alan多斜坡ADCv3

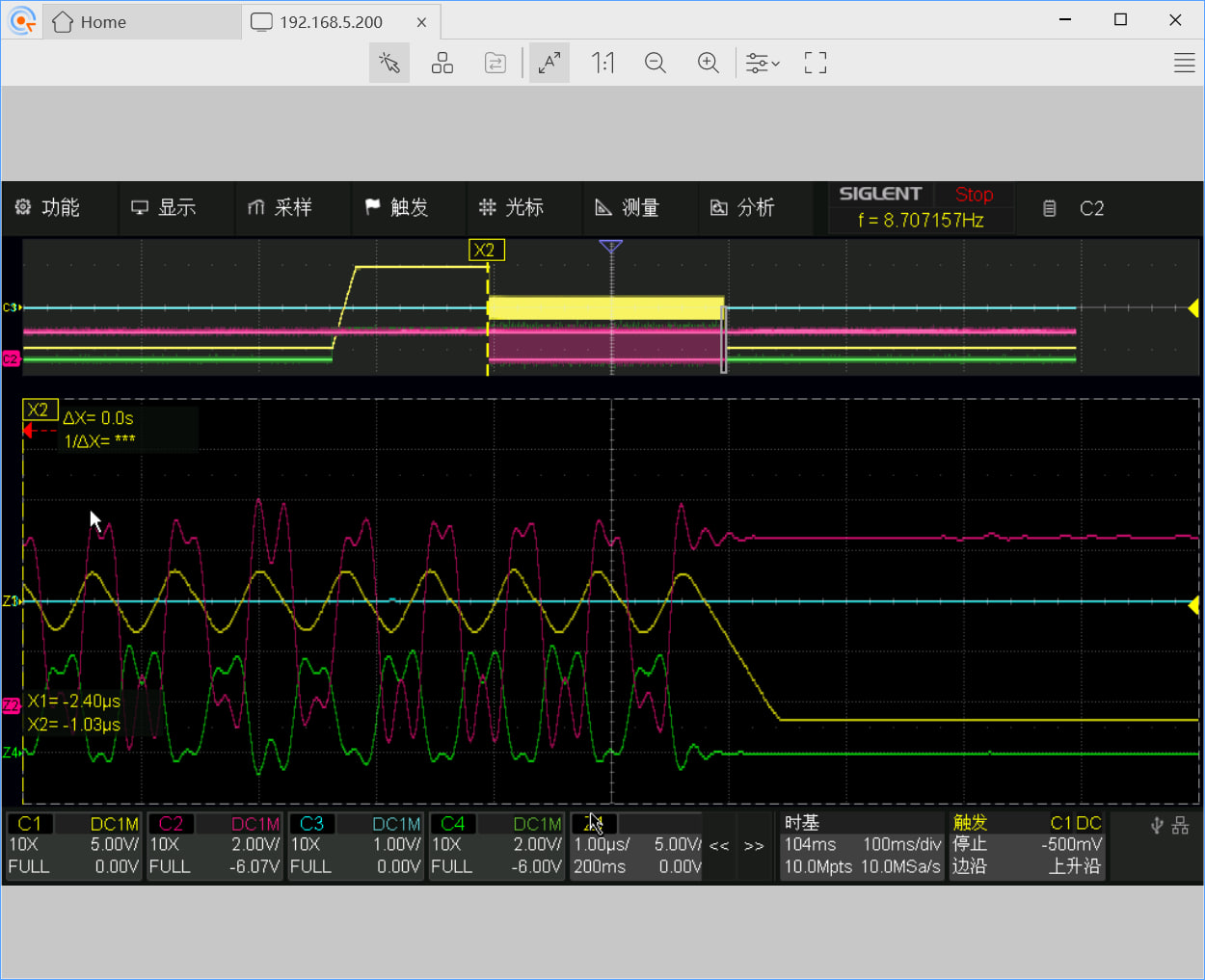
Alan多斜坡ADCv3整体模仿HP34401A，MAX10 10M08 FPGA控制，核心部分同v1，但是削减了FLASH ADC，比较器换用了TLV3202。电源部分使用了自制的SEPIC+CUK+后级LDO。版型改为MAX10 EVAL的Arudino样式拓展板。该板的主要问题为LT5400系列排阻接线异常，飞线后解决。

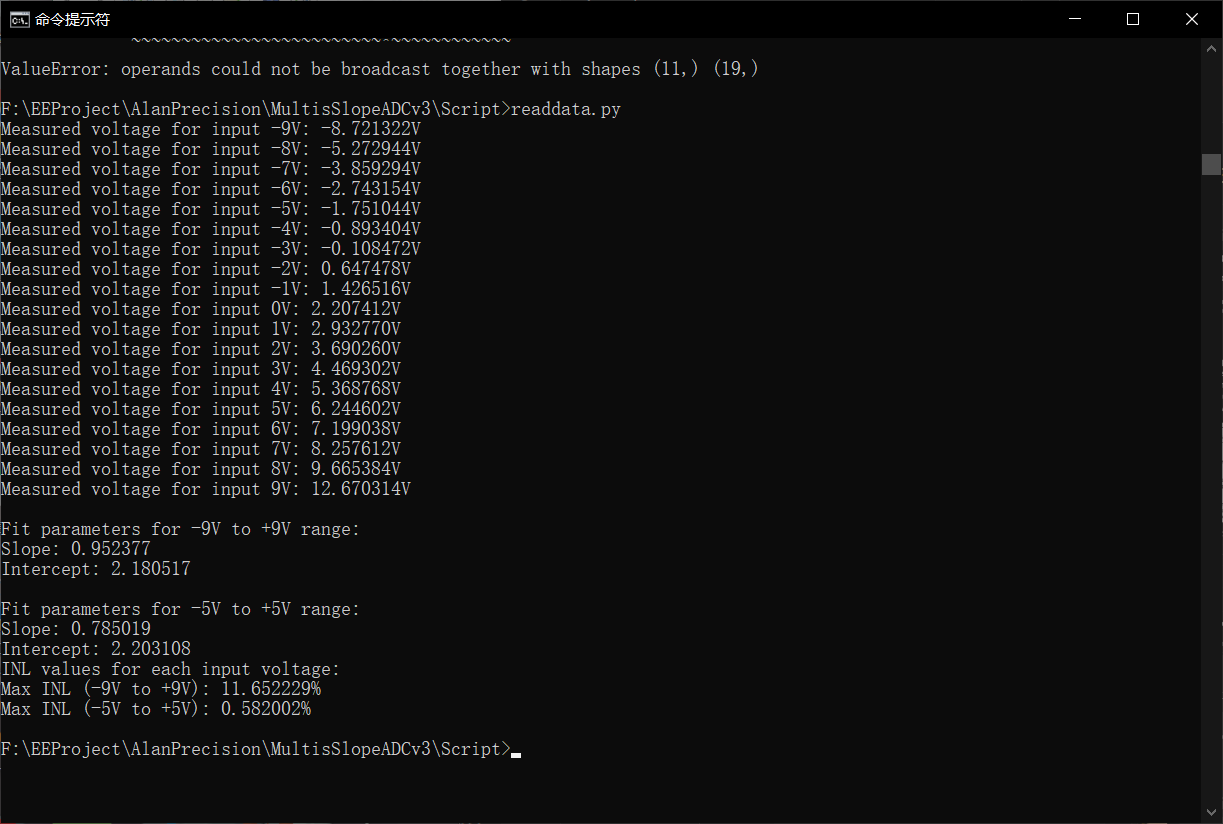
使用常规的bangbang控制，该版成功在10NPLC下实现了4位分辨率，在没有使用MOSFET非理想缓解开关模式的情况下，最大INL为0.58% 。该转换器在每次转换结束后通过串口发送二进制数据，以下是使用一个python脚本解码并计算INL的结果：

源码：https://github.com/AlanCui4080/MultiSlopeADCv3